Tutorial: Solutions of rods with SEB

Contributors: Carsten Svaneborg (FKF SDU).

Illustration of isotroplic solution of rod-like molecules.

Before you start

Download and install Scattering Equation Builder (SEB)
Complete the polymer tutorial to understand how SEB works and how scattering from a Gaussian polymer model is derived.

Learning outcomes

In this tutorial you will learn about the scattering from dilute isotropic solutions of rods, in particular

how to calculate the form factor of a rod,
and how the scattering from a stiff rod differs from a random walk polymer.

Rods

A rod is a simple geometric model of stiff molecules such as actin and microtubuli. Later we will also be using it as a building block in SEB to make more complicated structures.

Derivation of the scattering from a rod

We think of a single straight thin rod of length $b$ in a solution, where each point on the rod is a point scatterer, then the form factor can be stated as

$$F(q) = \left<\frac{\sin(q r)}{qr} \right>_P, $$

which is known as the Debye Formula. Since the rod can be oriented in any direction, the form factor only depends on the magnitute of the momentum transfer $q$, and the scattering pattern will be axis symmetric around the direct beam.

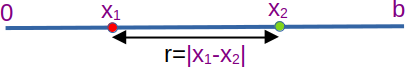
Sketch of rod showing the meaning of the symbols.

The rod is straight, hence the probability $P$ denotes the probability of two random scatterers on a straight line being a distance $r$ apart. We randomly pick one scatterer from an uniform distribution in the interval $[0,b]$. Thus $P(x_1)=1/b$ for $x_1\in [0,b]$ and zero elsewhere. This corresponds to the integral $ \int_0^b \frac{dx_1}{b} \cdots$. We pick the second scatterer $x_2$ from the same distribution, and with these two scatterers the distance between them is $r=|x_1-x_2|$, because the rod is straight. Thus the average corresponds to performing the following integrals:

$$ F(q) = \int_0^b \frac{dx_1}{b} \int_0^b \frac{dx_2}{b} \frac{\sin(q |x_1-x_2|)}{q|x_1-x_2|},$$

unfortunately the result of these integrals can not be expressed as a combination of the usual functions we know. The result is $$F(q)=\frac{2(\cos(x)-1+x Si(x))}{x^2}$$ where $x=qb$ and $Si(x)=\int_0^x dt sin(t)/t$ is the sin integral function. This function has to be evaluated numerically and SEB can do this.

Scattering Equation Builder (SEB)

Scattering Equation Builder (SEB) is a C++ library for analytical derivation of form factors of complex structures. The structures are build out of basic building blocks called sub-units. Polymers and rods are two of the sub-units supported by SEB.

Before you can use SEB you need to install a working C++ compiler, the GiNaC, GSL, and CLN libraries, and the SEB source code itself. See GitHub for the details of how to install SEB on various operating system. Important you need to remember the folder, where you put the SEB source code. It has a subfolder "work" where you can save and compile your own programs.

Rods with SEB

To calculate the form factor of a rod, cut'n'paste the following C++ program into an text editor (e.g. notepad). Save it as "Rod.cpp" in the work folder under the SEB installation.


// Include SEB functionality
#include "SEB.hpp"

int main()
{
    // Create world of sub-units
    World w("World");

    // Add a single rod-subunit named "A"
    GraphID r = w.Add(new ThinRod(), "A");

    // Wrap unit in a structure named Structure (this will make sense later)
    w.Add(r, "Structure");
    
    // Print out equation for the form factor
    ex F=w.FormFactor("Structure");
    cout << "Form Factor= " << F << "\n"; 
    
    // To evaluate the equation, we need to define value of paramters
    ParameterList params;
    w.setParameter(params,"L_A",XXX);     // Lengths of the "A" rod
    w.setParameter(params,"beta_A",1);    // Scattering length
    
    // Choose q values
    DoubleVector qvec=w.logspace(0.01, 10.0, 1000 );

    // Use Evaluate to save form factor data to a file
    w.Evaluate( F, params, qvec, "formfactor_rod.q", "Form factor of a rod with beta=1 and L=1.");   
}

Exercise 1 compare the form factor of a rod and a polymer

In exercise 2 of the Gaussian Polymer you generated a file "formfactor_polymer.q" with the form factor of a polymer. For large $q$-values we observed $F(q)\sim q^{-2}$ where $2$ happens to be the fractal dimension of a random walk.

1a: The code above calculates the form factor of a rod. Bold face indicates the important changes made wrt. the polymer code. The radius of gyration of a rod is $R_g^2=b^2/12$, where $b$ is the length of the rod. Change the length of the rod indicated by $XXX$, such that the radius of gyration of the rod matches that of the polymer. Run the code as you did in the Polymer example
1b: Sketch what you expect a log-log plot of the form factors of a rod and a polymer looks like for small and large $q$ values. (Hint: A rod has fractal dimension $1$.) Then make the plot of the files produced by SEB to see whether they agree with your sketch.

Home

All SEB tutorials