Calculating small-angle scattering of an object using randomly distributed points

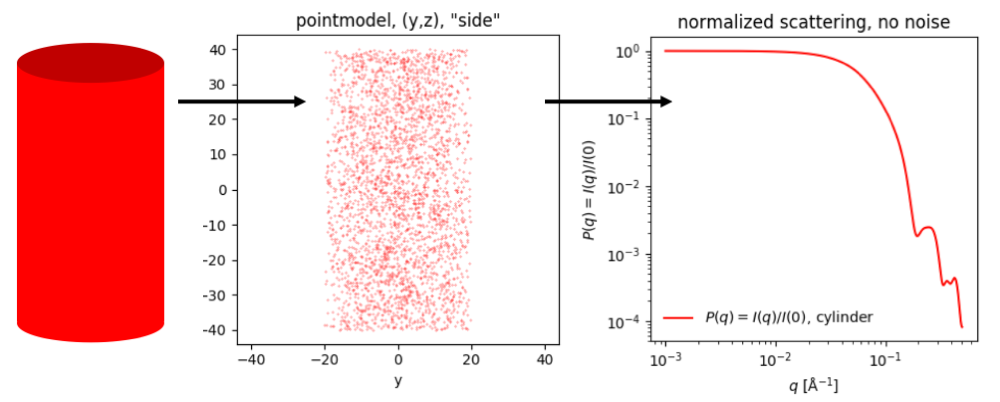
SAXS and SANS data from a particle, e.g. a cylinder, can be simulated using various methods. One of them, used by Shape2SAS, is to fill the cylinder volume by randomly distributed points (or small spheres). The scattering can then be calculated by the Debye equation.
If enough points are fill into the volume, the scattering from these points corresponds to the scattering from the cylinder. It is a bit like pixels in an image: if the resolution is good enough (enough pixels), you do not see the pixels.
The $q$-value defined which size we probe: small $q$ are large distances, and large $q$ probe small distances. So the larger $q$, you would like to simulate, the more points you need to fill into the cylinder volume. A cylinder is in fact a poor example, as the scattering from a cylinder can be calculated analytically, which is faster than than filling with points, but other shapes may not have an analytical expression. This could, e.g., be the envelope of a protein.