Home

Tutorial: Core-shell Form factor

Contributors: Andreas Haahr Larsen.


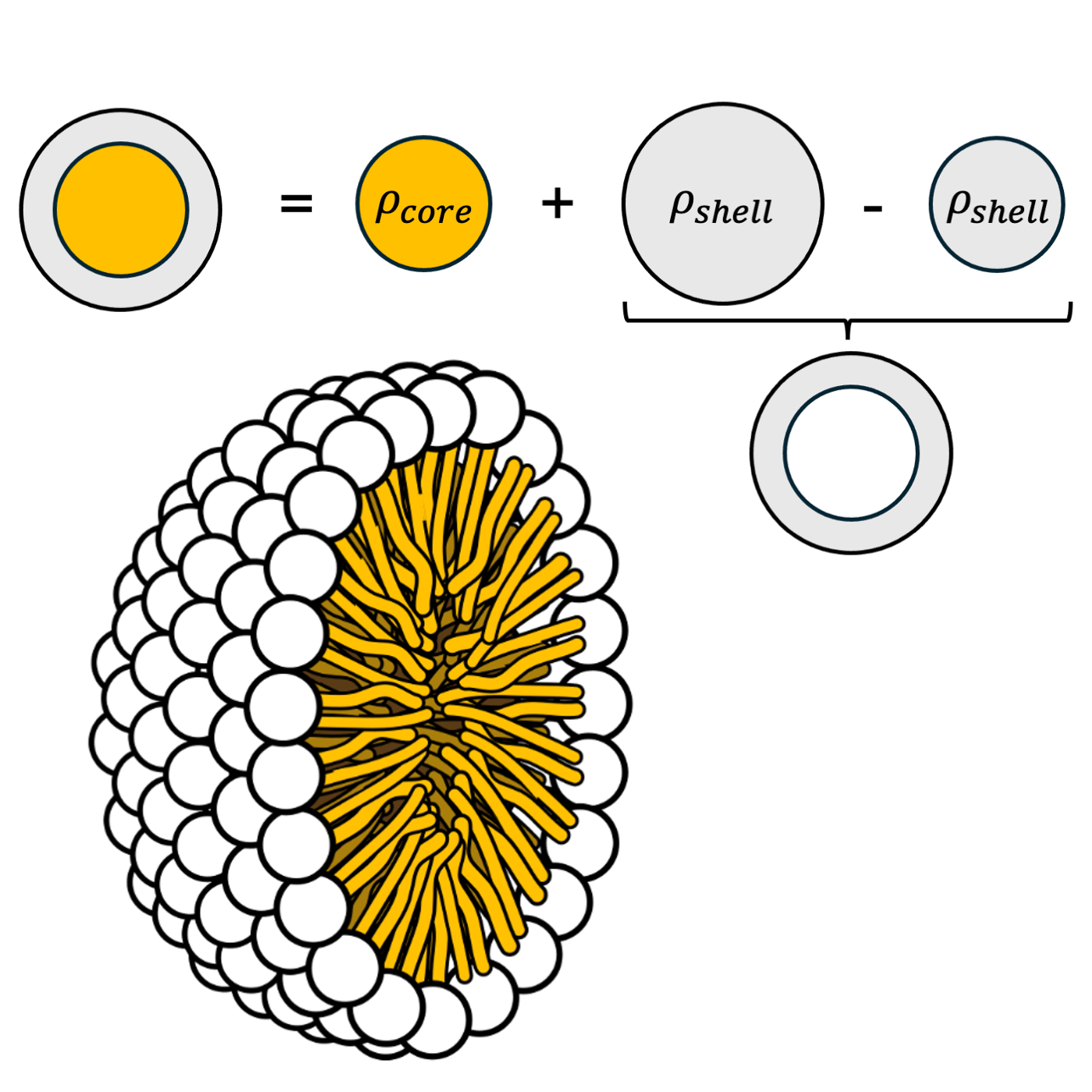
A form factor of a spherical core-shell particle (e.g. a micelle) can be build up as a combination of sphere form factor amplitudes. Micelle illustration from Wikimedia Commons.

Before you start

  • You will need pen and paper

Learning outcomes

Learn how to build up complex scattering form factors
  • Learn the steps of building up form factors
  • Be able to put together spherical form factor amplitudes to derive the form factor for a spherical core-shell particle
  • Be familiar with different notations and terminologies

Introductory remarks

Form factors describe the scattering from a given particle, and depends on its shape and size. The form factors can be derived as an integral over the scattering length density over the particle volume. Luckily, this has been done for many particles already in the litterature (Pedersen, 1997).
However, if the scattering from your particle of interest is not yet described, it is possible to build up new form factors from existing. In this tutorial, you will build up a (simple) micelle form factor.

Part I: Determine the simplest possible geometric shape that represents the micelle

A micelle is complex, composed of many lipids and or detergents. However, in small-angle scattering the important part is the scattering length density (relative to the solvent), $\Delta\rho$. For SAXS this is determined by the electron density. Lipids are caracterised by a headgroup, with a high electron density (containing heavy atoms), and a tail with low electron density (mostly CH2).
Use this information to think of a simple shape that can represent a micelle. You can check you answer with this answer.

Part II: Find the relevant subunit and its form factor amplitude

A form factor can be built up of subunits with known form factor (amplitude). There are various sources for finding form factors (e.g. Pedersen, 1997).
Find the form factor amplitude for a sphere in the Pedersen1997 paper (if you square the form factor amplitude, you get the form factor).
You can check you answer with this answer.

    A note (warning) on notation:
  • Some authors use the form factor, $P(q)$, to denote the form factor amplitude, $F(q)$, and various letters are used for both, but most authors use $P(q)$ for the form factor.
  • Most authors normalize $P(q)$, such that it is unitless, and such that $P(q=0)=1$, but this is not always the case, so $P(q)$ sometimes has units.
  • The atomic form factor is an important example of not following the notation used in this tutorial. The atomic form factor, $f_a(q)$, conventionally denotes the form factor amplitude of an atom, e.g. carbon, $f_c(q)$. It is normalised, so $f_a(q=0)$ is equal to the number of electrons times the electron scattering length, $b_e$, e.g. $f_c(q=0)=6b_e$.

Part III: Calculate the weighted average to get the micelle form factor amplitude

To get the form factor for the whole particle (core-shell micelle), you need to add the form factor amplitudes and take the absolute square. The terms needs to be weighted correctly, with the excess scattering length density, $\Delta SLD$ (also called contrast) and volume, $V$. For the volume see this hint.
Note that for the shell, you need to subtract the spherical core from a sphere to form a spherical shell.
Generally, a weighted average of $a,b,c$ weithed with weights $w_a,w_b,w_c$ is: $$ \frac{w_a a + w_b b + w_c c}{w_a + w_b + w_c} $$ Now, make the weighted average of the form factor amplitude of a micelle, $F(q,r,R,\Delta\rho_h,\Delta\rho)$, weithed with $\Delta\rho V$ to get the form factor amplitude of the micelle. You can check you answer with this answer.

Part 3: Calculate the form factor

This is by far the easiest part. When you have the form factor amplituede, you can calculate the form factor at the absolute square: $$ P_\mathrm{coreshell}(q) = |F_\mathrm{coreshell}(q)|^2 $$ easy!

Part IV: Make a strategy for verifying the model

One way to verify the model is to implement the model, e.g. in SasView. You can then fit against simulated data (where you know the true parameter values). See how this may be be done in the core-shell tutorial.
Another important aspect is to check the normalization is correct: $P(q=0)=1$?

Challenges

  1. Challenge 1: Derive the form factor for a spherical shell with thickness $T$.
  2. Challenge 2: Derive a form factor for a spherical core-shell particle with one core and two concentric shells.

Help and feedback

Help us improve the tutorials by
  • Reporting issues or bugs via our GitHub page (including typos, dead links etc.), but also insufficient information or unclear instructions.
  • Suggesting new tutorials/additions/improvements in the SAStutorials forum.
  • Posting or answering questions in the SAStutorials forum.

Home