Home

Tutorial: Contrast Variation

Tutorial contributors: Andreas Haahr Larsen

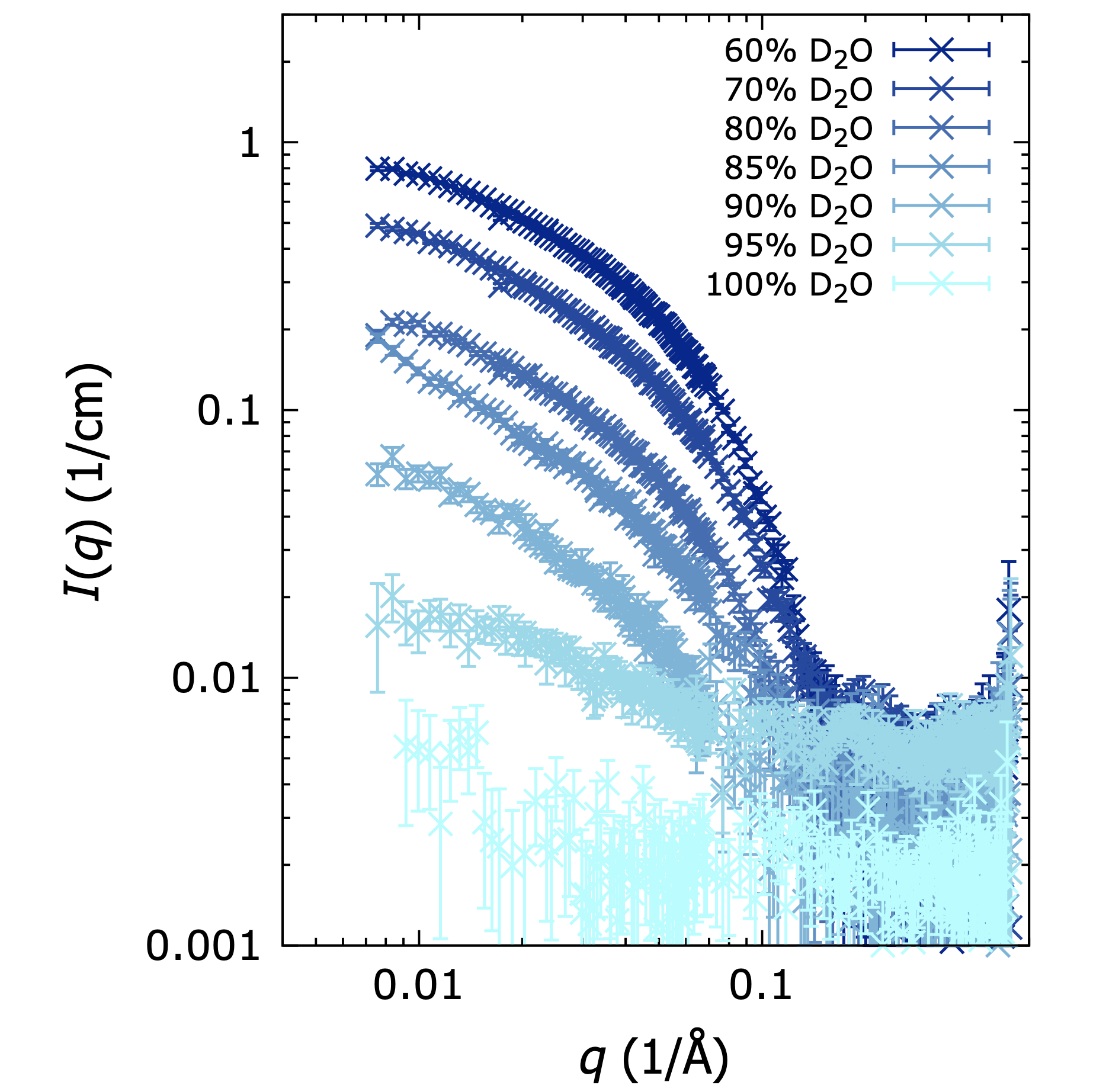
Partly deuterated detergent DDM, measured in SANS with various amoumts of D₂O in the solvent. At 100 D₂O, the DDM molecules are matched out. Adapted from Midgaard et al., 2018, FEBS J. 285: 357-371, with permission.

Before you start

• Download and install SasView (on MacOS: you need to install Xcode first).
• We recommend that you first complete the Spheres tutorial if you are not familiar with basic fitting in SasView.

Learning outcomes

Be able to design a contrast-variation experiments in SANS for structure determination. Specifically, you will be able to:
• Explain what contrast is in small-angle neutron scattering (SANS).
• Explain the relationship between contrast and signal-over-noise in SANS data.
• Tune contrasts of a particle such that the forward scattering is zero.
• Fit SANS data from multicontrast particles, and understand how to avoid parameter correlation.
• Calculate scattering lenghts, scattering length densities and contrasts for a molecule, and use this to design a contrast-match experiment.

Part 1: Monodisperse spheres with various contrasts

Go to: Shape2SAS, and simulate a spheres with a radius of 50 Å and contrast (excess scattering length density, $\Delta\mathrm{SLD}$) of 1 as Model 1, and a sphere with contrast $\Delta\mathrm{SLD}-1$ as Model 2 (set parameters and press Submit):

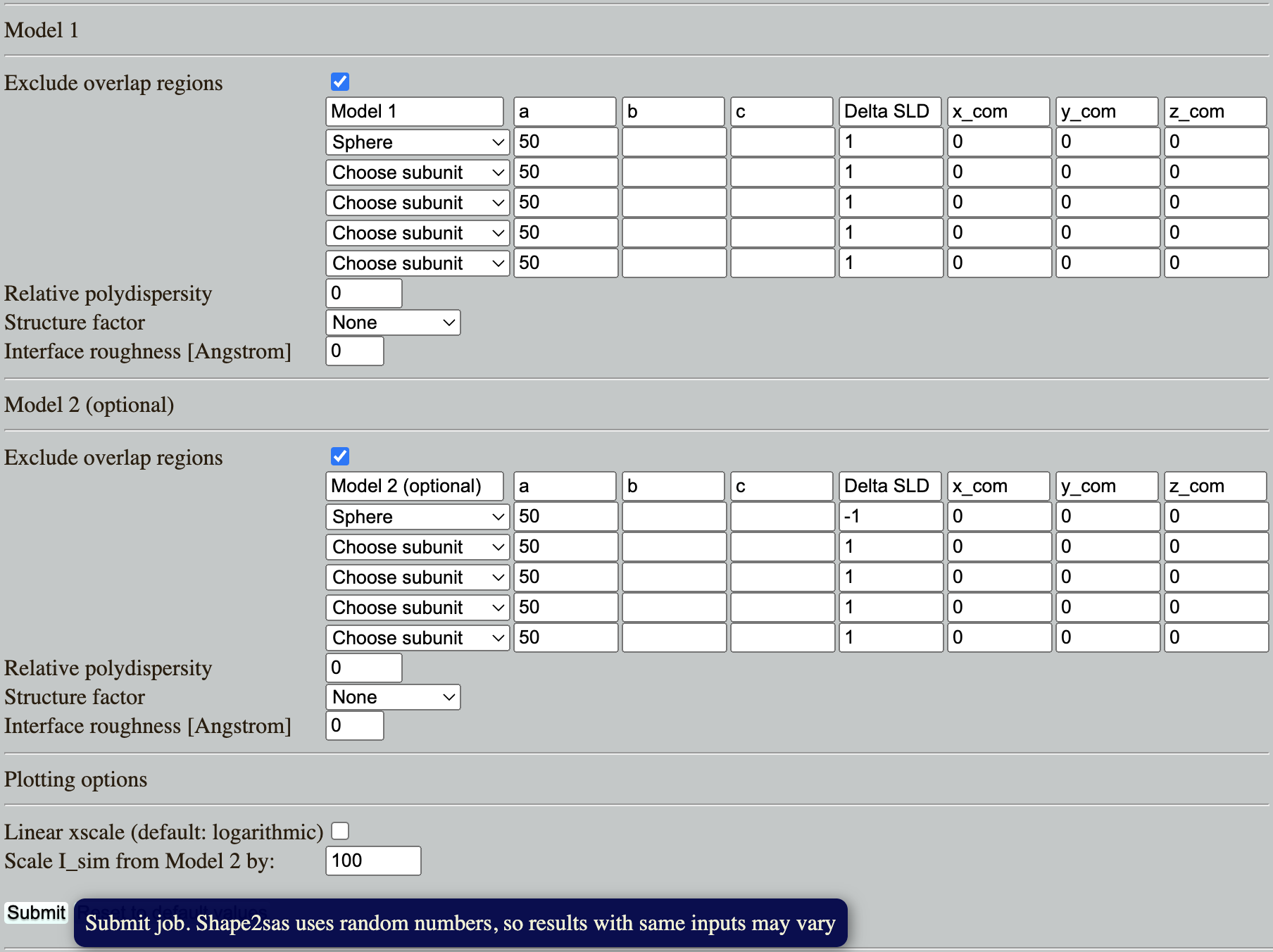
Comment on the resulting scattering. Why is the scattering the same despite that the $\Delta\mathrm{SLD}$ have opposite sign? (Hint)
Try to vary the contrast. How does a numerically larger ΔSLD affect the simulated scattering, and why? (Hint)
Take-home message: higher contrast gives a larger signal-over-noise, and is therefore preferable.

Part 2: Core-shell spheres

Go to: Shape2SAS, and simulate a spherical core-shell particle with inner radius of 30 Å and core $\Delta\mathrm{SLD}=-1$, and outer radius of 50 Å and shell $\Delta\mathrm{SLD}=1$. This can be done by combining two spheres as Model 1 (important: the smaller should be above the larger in the list, so the overlapping region is excluded from the larger sphere):

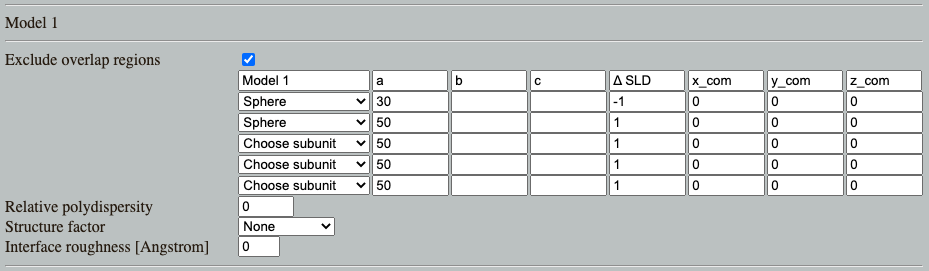
Try to compare with spheres with radii 30 Å and 50 Å (as Model 2 and 3). What combination of radii of the core-shell (Model 1) would yield $I(0)$ of 0? (Hint). Try to simulate this. Due to the stochastic nature of Shape2SAS, $I(0)$ may not be exactly 0, but will be small.
Download the simulated data for the core-shell particle (Model 1): Isim.dat (example data), load it into SasView and fit a core-shell sphere form factor. Assess if it is good fit, and if paramters are correlated.

Assessing if a fit is good:
• Does the fit look resonable - i.e. does the fitted curve go through the data points, within the errors. Is the fit good in the whole $q$-range?
• Is the $\chi^2$ close to unity? This is a measure for the goodness of fit.
• Does the residuals look alright, or are there visible systematic deviations?
• Are the fitted values in the expected range? The true values are not known in an experiment, but you will usually have some idea about what values are "reasonable".

Correlated parameters:
• Two parameters are (partly) correlated if a change of the scattering curved induced by changing one of these parameters can be (partly) cancelled by changing the value of the other parameter.
• If you fit correlated parameters simultanaously, you will observe high uncertainties on the parameters values.
• In this example, the SLD values are correlated (due to Babinet's prinicle). That is, you can fit the data equally well with different combinations of SLD_core, SLD_shell and SLD_solvent - as long as the contrasts are unchanged. The SLD values are also partly correlated with the scaling parameter.
• Consequently, if you fit multiple SLD values (and scaling), you will observe large uncertainties on these parameters (example).
• To prevent correlation, you can restrict the fit by fixing parameters. For this reason, SLD_solvent is usually fixed, and in this example, you should also fix either SLD_core or SLD_shell if scaling is fitted.

Part 3: Match-out DDM in 100% D₂O

The goal of this subpart is to calculate how much to deuterate a DDM detergent in order to match it out in a SANS experiment at 100% D₂O. This can be done by following these steps:

1. Use the chemical formulas to calculate the neutron coherent scattering lenghts for heavy water (D₂O), DDM headgroups (C₁₂H₂₁O₁₁) and DDM tailgroups (C₁₂H₂₅), using NIST tabular values (step-by-step guide for calculating SL for D₂O).
2. Use experimentally determined molecular volumes to calculate scattering lenghts densities $\mathrm{SLD}=SL/V$ and contrasts $\Delta\mathrm{SLD} = \mathrm{SLD}-\mathrm{SLD}_\mathrm{D2O}$ for heavy water (30.0 ų), DDM headgroups (350.4 ų) and DDM tailgroup (350.2 ų).
3. Put the results into a spreadsheet:
   
   
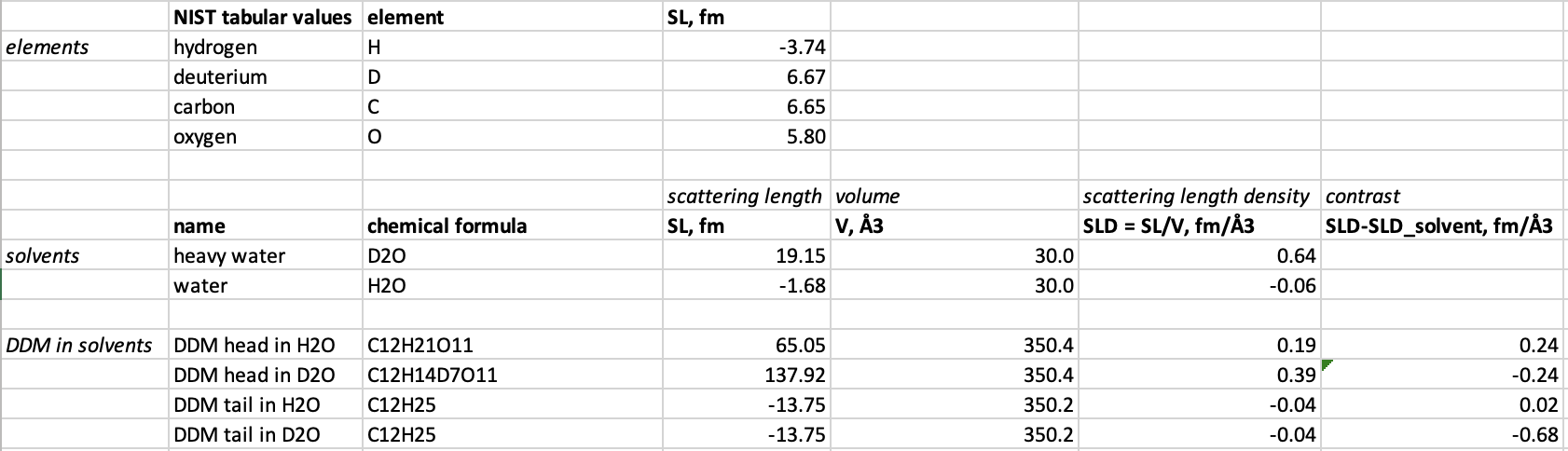
4. Take exchangable hydrogens in account, i.e., hydrogens that are not strongly bound, and become deuterium when DDM is submerged in D₂O.
   There are 7 exchangable Hs in the the DDM headgroup, but none in the tailgroup, as these hydrogens are tightly bound to the carbons.
   Calculate the $\mathrm{SLD}$ and $\Delta\mathrm{SLD}$ of the DDM headgroup after exchange (C₁₂H₁₄D₇O₁₁), where H denote non-exchangable hydrogen, and D denote hydrogen that have been exchanged with Ds from the solvent ("DDM head in D2O" in the spreadsheet above).
   
5. Now, calculate how many of the non-exchangable Hs that should be deuterated in the DDM head to match out these components, i.e. get zero contrast when solvated in D₂O ($\Delta\mathrm{SLD}=0$). For the head groups: $$SLD_\mathrm{head} = SLD_\mathrm{D2O}$$ $$SL_\mathrm{head} = SL_\mathrm{D2O}\frac{V_\mathrm{head}}{V_\mathrm{D2O}}$$ where $SL_\mathrm{head}=12SL_C+(14-n)SL_H+(7+n)SL_D+11SL_O$ and $n_\mathrm{head}$ is the average number of non-exchangable H's that should be deuterated: $$n_\mathrm{head} = (SL_\mathrm{D2O}\frac{V_\mathrm{head}}{V_\mathrm{D2O}}-12SL_C-14SL_H-7SL_D-11SL_O)/(SL_D-SL_H)$$
6. Repeat this for the DDM tail groups.

Once you are done, you may check with this filled-out spreadsheet (but try calculating everything before you look at the answer).

Incoherent scattering in SANS
Incoherent scattering contribute a constant scattering signal (i.e. the same in all directions). Therefore, it carries no structural information.
Therfore, it is generally better to measure samples in D₂O rather than in H₂O in SANS, due to incoherent scattering from hydrogen, which result in a poor signal-to-noise ratio.
If you want numerical values, you may follow the (step-by-step guide for calculating SL for D₂O), but use the inhoherent scattering lengths (Inc b) insted of the coherent scattering lengths (Coh b). Then you can calculate the total incoherent scatteirng lenght from the various components.

Challenges

1. PEGylated spherical metallic nanoparticle were measured with small-angle scattering. The PEGylation is expected to form a shell around the nanoparticle. The sample was measured with two different contrasts: in SAXS where the core contrast is much larger than the PEG contrast (SAXS data), and with SANS where the contrasts are more comparable (SANS data). What is the structure of the particle (inner and outer radii).
2. You are interested in the structure of a polymer chain, inside a polymer melt. I.e. a melt consisting of a lot of the same polymer chains. However, when measuring, you just get a flat (constant) signal. How do you approach the problem? Hint: contrast variation may help.
3. You would like to contrast-match the phospholipid DLPC in D₂O, in order to measure membrane proteins in an invisible lipid bilayer with SANS. Headgroup phospotidylcholine (PC) has the chemical formula C₁₀H₁₈NO₈P (6 of these hydrogens are exchangable) and volume a of 319 ų. The tail group dilauroyl (DL) has the chemical formula C₂₂H₄₆ (no exchangable hydrogens) and a volume of 666 ų. How many of the (non-exghangeable) hydrogens should be deuterated in, respectively, head and tail to match-out DLPC in a solvent of 100% D₂O?

Feedback

By filling this feedback form you can help us improve the tutorials (it takes 2 min).

Home